L'arithmétique est la partie de la mathématique qui étudie les nombres. Depuis toujours, les mathématiciens se sont intéressés aux propriétés des entiers naturels, et l'on trouve dans les Eléments d'Euclide (IIIe siècle av. J.-C.) un traité assez complet d'arithmétique élémentaire.
L'écriture des nombres
Les problèmes posés par
l'écriture des nombres ont été diversement résolus au cours des âges. Notre
système décimal actuel a été introduit, dans son principe, par les Hindous aux
VIe et VIIe siècles ap. J.-C., et nous fut transmis par
les Arabes.
Le boulier ou abaque sert à compter les points dans un jeu.
En Chine, où il remonte au IXe siècle avant notre ère, le
souan-p'an est encore utilisé par les commerçants. Il recourt au principe
même de la "bijection", correspondance terme à terme entre les éléments de deux
ensembles.
Dans le système décimal, nous utilisons dix chiffres, de 0 à
9, pour écrire les nombres, les unités s'écrivant avec un chiffre, les dizaines
avec deux chiffres, les centaines avec trois.
Pour écrire un nombre - ou pour compter - nous effectuons des
groupements réguliers en procédant par étapes. On groupe ainsi par dix tous les
objets, jusqu'à ce que l'on ne puisse plus faire de "paquets" de dix; les objets
restant sont alors en nombre inférieur à dix. Puis on recommence en groupant par
dix les paquets de dix, afin de faire des "paquets" de cent, et l'on s'arrête
lorsqu'il reste moins de dix paquets de dix. Et l'on recommence encore en
groupant par dix les paquets de dix paquets de dix. L'écriture "3 025" signifie
qu'il reste cinq paquets à la première étape, puis deux paquets de dix, puis
zéro paquets de cent, trois paquets de mille.
Le système décimal utilise dix comme "base de la numération".
Mais il est possible, avec le même procédé, de choisir une autre base. Ainsi,
dans le calcul binaire, la base choisie est deux, et les groupements effectués
sont de deux à chaque étape. Prenons un autre exemple : si on choisit six comme
base de numération, on effectue des groupements de six. En utilisant les six
chiffres : 0, 1, 2, 3, 4, 5, l'écriture "2 403" signifie qu'il y a deux paquets
de six fois six fois six objets, quatre paquets de six fois six objets, zéro
paquets de six objets et trois objets.
Les nombres premiers
Les nombres premiers jouent un
rôle fondamental en arithmétique. Un nombre est dit "premier" si ses seuls
diviseurs sont 1 et lui-même. Il en est ainsi des nombres 2, 3, 5, 7, 11, etc.;
par contre un nombre tel que 10 n'est pas premier, ses diviseurs sont 1, 2, 5 et
10.
On peut démontrer que la liste des nombres premiers est
illimitée; mais il n'existe pas de procédé simple pour trouver un nombre premier
de rang donné, par exemple le cinquantième. Pour établir la liste des nombres
premiers compris entre 0 et un nombre n quelconque, on peut utiliser le
crible d'Eratosthène. Prenons le cas où n est égal à 100 : il est
commode de disposer les nombres en carré et on barre successivement tous les
multiples de 2 (nombres pairs) puis les multiples de 3, puis de ceux de 5, puis
ceux de 7; les multiples de 4, 6, 8, 9 et 10 sont alors barrés, et il est
inutile de continuer au-delà.
L'importance des nombres premiers tient à trois séries de
propriétés :
1. Tout nombre peut s'écrire de manière unique comme produit de nombres premiers
élevés à une certaine puissance. Par exemple, on a :
72 = 2 x 2 x 2 x 3 x 3 = 23 x 32
803 = 11 x 73
83 = 83
L'ensemble des nombres premiers (ensemble infini) permet donc de retrouver
l'ensemble des nombres entiers par multiplication.
2. Par la décomposition en facteurs premiers d'un nombre, on peut retrouver tous
ses diviseurs de manière simple. Ainsi 72 = 23 x 32; ses
diviseurs sont : 1, 2, 4 (= 22); 8 (= 23); 3, 6 (= 2 x 3);
12 (= 22 x 3); 24 (= 23 x 3); 9 (= 32); 18 (= 2
x 32); 36 (= 22 x 32); 72 (= 23 x 32).
Il est commode de représenter les diviseurs d'un nombre par un schéma montrant
comment ils sont divisibles les uns par les autres.
3. La décomposition des nombres en facteurs premiers nous donne un moyen simple
pour déterminer le P.G.C.D. (plus grand commun diviseur) de deux ou plusieurs
nombres ainsi que leur P.P.C.M. (plus petit commun multiple). Ainsi pour 750 et
180 on a :
750 = 2 x 3 x 53
180 = 22 x 32 x 5
2
x 3 x 5 = 30
est leur P.G.C.D.
23
x 32 x 53 = 4 500
est leur P.P.C.M.
La notion d'idéal dans les entiers relatifs
L'ensemble Z des entiers
relatifs (entiers positifs, négatifs ou nul), muni des opérations d'addition et
de multiplication, est un "anneau". Dans un anneau, on peut définir des
sous-ensembles particuliers appelés "idéaux", de la manière suivante : un
"idéal" dans un anneau est un sous-ensemble tel que : si deux éléments sont dans
un idéal, leur somme y est aussi; et le produit d'un élément de l'idéal par un
élément quelconque de l'anneau est un élément de l'idéal.
Une interprétation géométrique du plus
grand commun diviseur et du plus petit commun multiple des nombres 180
et 750. Leur P.G.C.D. est 30 : c'est ici le plus grand volume qu'ils
aient en commun. Leur P.P.C.M. est 4 500 : c'est le plus petit volume
les contenant que l'on puisse construire sur leurs arrêtes.
Dans l'anneau des entiers relatifs, l'ensemble des nombres
pairs est un idéal; de même l'ensemble des multiples de 3 (positifs, négatifs ou
nul) est un idéal; plus généralement, l'ensemble des multiples d'un nombre P
quelconque est un idéal dans Z. Réciproquement, on peut démontrer que dans
l'ensemble des entiers relatifs, tout idéal est de cette forme, c'est-à-dire que
tout idéal peut être considéré comme l'ensemble des multiples d'un nombre.
Cette propriété a les conséquences suivantes pour les
P.P.C.M. et les P.G.C.D. de deux nombres a et b :
l'ensemble M(a) des multiples de a est un idéal;;
l'ensemble M(b) des multiples de b est aussi un idéal; leur
intersection M(a) Ç M(b)
est un idéal ensemble des multiples du P.P.C.M. de a et de b.
De plus, l'ensemble des nombres de la forme "xa + yb" où x et
y peuvent prendre toutes les valeurs possibles dans Z est un idéal dont le
générateur est le P.G.C.D. de a et de b. Par suite, le
P.G.C.D. de a et de b est un nombre de la forme ci-dessus.
Enfin, si deux nombres sont premiers entre eux, c'est-à-dire que leur P.G.C.D.
est 1, il existe x et y dans Z tes que: "xa + yb = 1"
(théorème de Bézout).
Les énigmes de l'arithmétique
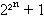Ces problèmes d'arithmétique
sont indépendant du système d'écriture des nombres utilisé. D'autres sont liés
au système de numération choisi, comme les critères de divisibilité par 4, par
9, etc.
De nombreux problèmes restent irrésolus et continuent de
susciter la recherche en théorie des nombres. Ainsi on ne sait pas trouver de
formule donnant le nième nombre premier; on ne sait pas plus trouver
d'expressions ne donnant que des nombres premiers. Le célèbre mathématicien
Fermat (1601-1665) avait un moment pensé que les nombres de la forme
étaient tous premiers. Il n'en est rien, car pour n = 5 on obtient :
Parmi les problèmes non résolus, on peut encore citer
celui-ci : existe-t-il, pour n donné, trois nombres entiers x, y et z tels que
l'on ait :xn + yn = zn?
Fermat pensait avoir démontré que ce problème n'a pas de solution pour n
supérieur ou égal à 3. Personne n'a jamais vu sa démonstration, et, depuis trois
siècles, les mathématiciens ont pu donner une démonstration pour n = 3, n = 4, n
= 5, n = 6, n = 7, mais ne lui ont pas donné une réponse générale.
